주기적 원자 배열과 역공간 이해하기: 제 1 브릴루앙 영역 (Brillouin Zone)

안녕하세요! 반도체 쉽게 알려주는 블로그 "띵주의 공부일기"입니다. 오늘은 반도체를 배우거나 연구하는 분들이라면 꼭 알고 있어야 할 주기적 원자 배열 구조와 역공간에 대해 깊이 있게 알아보겠습니다. 이 내용은 반도체가 어떻게 전기적 특성을 가지는지, 그리고 이러한 특성을 이용해 전류가 흐르는 원리를 이해하는 데 필수적인 개념입니다. 함께 천천히 살펴볼까요?

---

1. 원자 배열의 주기성과 에너지 장벽

반도체는 규칙적으로 배열된 원자들로 이루어져 있습니다. 이 배열은 마치 장난감 블록이 일정한 간격으로 쌓인 모습과 같습니다. 이렇게 주기적으로 배열된 원자는 전자가 이동할 수 있는 공간과 이동할 수 없는 공간을 만들어냅니다.

• 허용 에너지 대역 : 전자가 특정 에너지를 가질 경우 이동이 가능한 경로입니다.
• 금지 에너지 대역 : 반대로 에너지가 부족하거나 너무 높을 경우, 전자가 이동하지 못하는 경로입니다.

이 개념이 중요한 이유는 반도체가 금속(전기가 잘 통하는 도체)도 아니고, 고무처럼 전기가 거의 흐르지 않는 절연체도 아닌 독특한 성질을 가지기 때문입니다. 전압이나 에너지를 가하면 반도체는 허용 대역을 통해 전류를 흘릴 수 있습니다.

---

 

2. 역공간(k-space)와 주기성

역공간 (k-space) 이란?

원자 배열을 연구할 때, 우리는 단순히 물리적인 공간만 보는 것이 아닙니다. 대신, 원자 배열이 만들어내는 주기적인 패턴을 수학적으로 표현한 **역공간(k-space)**을 사용합니다.
또한, 실공간에서 주기적 원자 배열을 갖는 경우 역공간인 k공간에서도 주기적인 특징을 가집니다.

E-k 관계

• 역공간은 전자의 **에너지(E)**와 운동량(k) 간의 관계를 나타냅니다.
• 이를 통해 우리는 전자가 주어진 에너지에서 어떤 특성을 가지는지, 어떤 속도로 이동할 수 있는지 알 수 있습니다.

중요한 이유

역공간은 전자 이동의 기본 원리를 이해하는 데 매우 중요한 도구입니다. 반도체 내에서 전자의 움직임을 예측하고, 특정 전압이나 온도 조건에서 반도체가 어떻게 작동할지를 알 수 있습니다.

---

3. 제 1 브릴루앙 영역 (Brillouin Zone)

k 공간에서 최소단위셀의 하나인 위그너-자이츠 셀을 정의한 제 1 브릴루앙 영역을 이용하여 전자의 특성을 이해하면 편리합니다. (위그너-자이츠 셀은 이전 post에서 다루었습니다.)

https://ddingjoo.tistory.com/entry/Day6%EC%9C%84%EA%B7%B8%EB%84%88-%EC%9E%90%EC%9D%B4%EC%B8%A0-%EC%85%80Wigner-Seitz-Cell-%EA%B2%B0%EC%A0%95-%EA%B5%AC%EC%A1%B0%EB%A5%BC-%EC%9D%B4%ED%95%B4%ED%95%98%EB%8A%94-%ED%8E%B8%EB%A6%AC%ED%95%9C-%EB%8F%84%EA%B5%AC

 

제 1 브릴루앙 영역은 고체 물리학에서 원자의 주기적 배열(격자 구조)을 이해하는 데 중요한 개념으로, 역공간(k-space) 내에서 가장 기본적인 단위 영역을 말합니다. 이는 반도체, 금속, 절연체 등 고체의 전자 구조와 에너지 대역(Energy Band)을 분석하는 데 필수적인 도구입니다.

(1) 제 1 브릴루앙 영역의 정의

제 1 브릴루앙 영역은 다음과 같이 정의됩니다:

• 격자의 역공간에서 가장 가까운 점들을 연결한 다각형 또는 다면체입니다.
• 이는 주기적 구조를 가진 물질의 역공간에서 가장 작은 단위로, 원래의 주기성을 보존하며 다른 모든 역공간 정보가 이 영역 안에 포함됩니다.

쉽게 말하면:

제 1 브릴루앙 영역은 원자 배열의 대칭성과 주기성을 반영한 역공간의 "최소 반복 단위"라고 할 수 있습니다.

(2) 제 1 브릴루앙 영역과 역격자

제 1 브릴루앙 영역은 **역격자(Reciprocal Lattice)**의 기본 개념과 밀접하게 관련되어 있습니다.

• 역격자는 원자 배열(실공간)의 주기적 성질을 수학적으로 표현한 것입니다.
• 역격자의 모든 점은 원자 배열의 대칭성과 일치하며, 이러한 역격자의 가장 기본적인 단위가 제 1 브릴루앙 영역입니다.

비유로 이해하기:

• 실제 원자 배열(실공간)을 벽지 무늬라고 한다면, 역격자는 그 무늬를 나타내는 반복 패턴의 지도와 같습니다.
• 제 1 브릴루앙 영역은 이 지도에서 가장 작은 반복 패턴입니다.

(3) 제 1 브릴루앙 영역의 구성

• 제 1 브릴루앙 영역은 Wigner-Seitz Cell을 역공간에서 정의한 것으로, 가장 가까운 대칭 점들을 기준으로 구분됩니다.
• 이 영역은 **에너지 대역(E-k 다이어그램)**의 계산 및 분석에서 중요한 역할을 합니다.

2차원 예시:

• 2차원 정사각형 격자에서, 제 1 브릴루앙 영역은 정사각형 형태를 띱니다.
• 2차원 육각형 격자(예: 그래핀)에서는 육각형 형태의 제 1 브릴루앙 영역이 만들어집니다.

3차원 예시:

• 3차원 체심입방격자(BCC): 브릴루앙 영역은 3차원에서 정육면체와 비슷한 구조를 가집니다.
• 면심입방격자(FCC): 브릴루앙 영역은 8면체와 비슷한 구조를 가집니다.

(4) 제 1 브릴루앙 영역의 물리적 의미

• 제 1 브릴루앙 영역은 고체 내에서 전자의 운동을 설명하는 E-k 관계를 해석하는 기본 단위입니다.
• 이 영역 내의 점들은 전자의 에너지와 운동량을 나타내며, 이를 통해 반도체의 전기적 및 광학적 특성을 분석할 수 있습니다.

대칭성과 대역구조:

• 대칭점(예: Γ, X, L 등)은 제 1 브릴루앙 영역의 중요한 위치를 나타내며, 대역구조(Band Structure) 해석에서 핵심적인 역할을 합니다.
• 각 대칭점의 에너지는 전자의 이동과 소자 특성(예: 전도성, 밴드갭 등)에 직접적인 영향을 줍니다.

k공간에서 제 1 브릴루앙 영역 (a) 실공간에서 FCC 구조 2개가 겹친 주기적 에너지 원자 배열 구조인 3차원의 다이아몬드 구조 (b) 실공간에서 FCC에 대한 역공간의 주기함수인 BCC 의 위그너-자이츠 셀(제1 브릴루앙 영역)

---

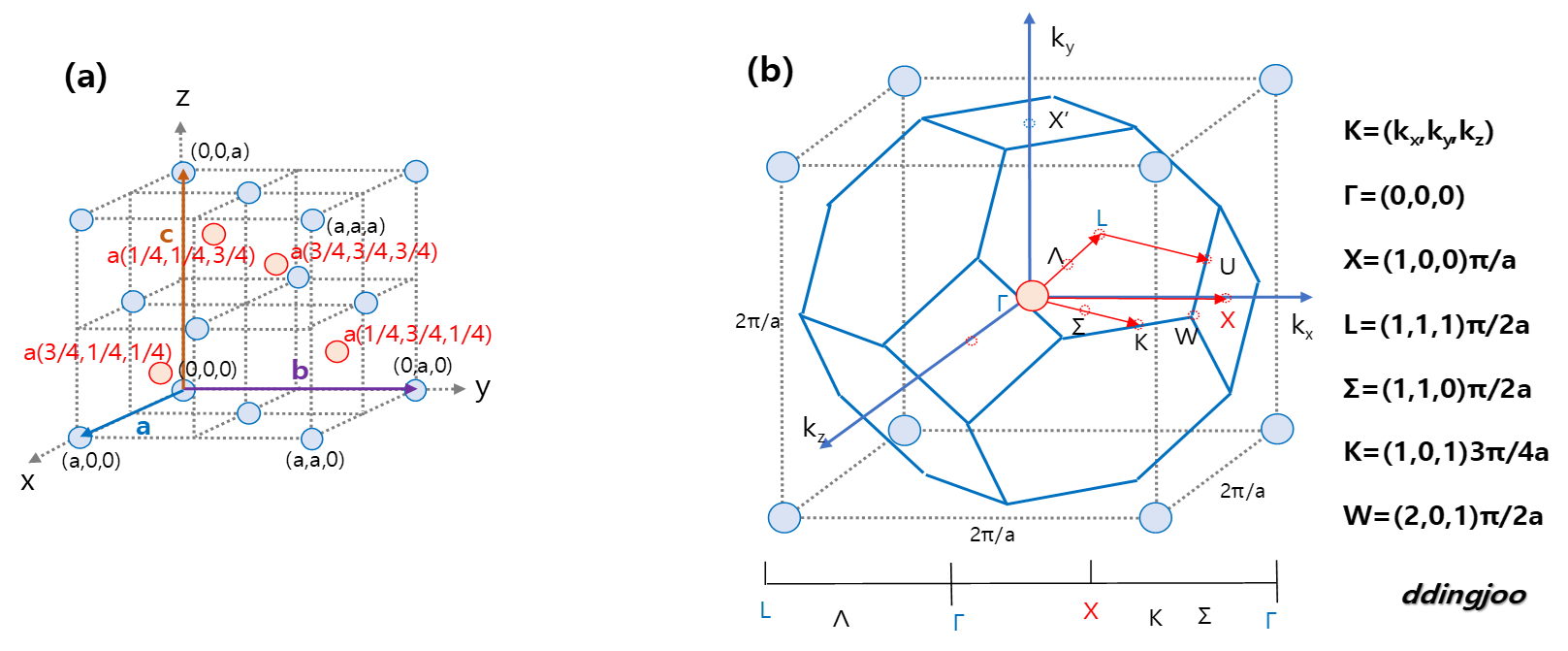
4. 쉽게 이해하는 제 1 브릴루앙 영역

• 제 1 브릴루앙 영역은 역공간에서의 최소 단위 셀입니다.
• 이 공간은 실제 공간(실공간)의 주기적 성질을 반영하며, 전자의 에너지 대역과 운동량 분석에 필수적인 역할을 합니다.
• **역격자의 중심점에서 가장 가까운 대칭점들로 구성된 다각형(2D) 또는 다면체(3D)**라고 이해할 수 있습니다.

---

마무리하며

따라서 3차원 원자 배열에 대한 E-K 관계를 그래프로 시각화하여 해석하는 방법은 크게 다음의 두 가지 방법이 있습니다.

1) 동일한 에너지를 갖는 k값들의 조합을 표시하는 동일 에너지 평면(equi-energy surface)의 변화를 이용하여
해석하는 방법
2) 위에 그림에서 나타낸 바와 같이 제1 브릴루앙 영역의 대칭성을 이용하여 해석하는 방법

제 1 브릴루앙 영역은 고체 물리학과 반도체 공학에서 가장 기초적이지만 중요한 개념입니다. 이를 통해 우리는 전자의 이동과 에너지 분포를 더 깊이 이해하고, 반도체 소자를 설계하거나 성능을 분석하는 데 필요한 기초를 쌓을 수 있습니다.

오늘 포스팅한 내용이 너무 어렵다면, 이것만 기억하세요!
실공간에서 주기적 원자 배열을 갖는 경우 역공간인 k공간에서도 주기적인 특징을 가진다.

 

다음에도 더 흥미로운 반도체 이야기를 들고 오겠습니다! 질문이 있다면 댓글로 남겨주세요.