반응형
안녕하세요, 여러분! 오늘은 양자역학에서 중요한 개념 중 하나인 1차원 무한에너지 장벽에 대해 이야기해보겠습니다. 이 개념은 전자가 특정 공간에 갇혀 있을 때의 특성을 설명하는 이론으로, 반도체 기술과 나노 기술의 이해에 꼭 필요한 내용입니다. 조금 어렵게 느껴질 수도 있지만, 쉽게 풀어서 설명드릴게요! 😊
1. 무한에너지 장벽이란?
무한에너지 장벽은 전자가 특정한 공간 안에 갇혀 있다고 가정하는 모델입니다.
- 전자는 이 공간(예: 0 ≤ x ≤ a) 안에서는 자유롭게 움직일 수 있지만, 밖으로 나갈 수는 없습니다.
- 장벽 바깥은 무한히 높은 에너지로 막혀 있어서, 전자가 벗어날 가능성이 없어요.
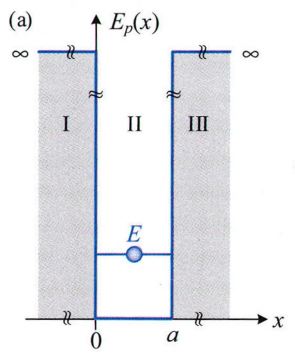
쉽게 말하면: 전자는 상자 안에 갇혀 있습니다. 이 상자 바깥으로 나가려고 하면 아주 강력한 벽에 막히게 되는 거예요.
2. 전자의 움직임과 파동함수
전자는 물결처럼 움직입니다. 이 물결을 수학적으로 표현한 것이 파동함수입니다. 파동함수를 통해 전자가 어디에 있을 확률이 높은지 알 수 있습니다.
(1) 파동함수의 특징
- 장벽 바깥에서는 0: 전자는 상자 밖으로 나갈 수 없으므로, 장벽 밖에서는 파동함수 ψ(x)가 0이 됩니다.
- 장벽 안에서는 물결 모양: 상자 안에서는 전자가 물결처럼 진동하며 움직입니다.
파동함수의 모양은 다음과 같습니다:

여기서 n은 양자수로, 전자의 에너지 상태를 나타냅니다.
3. 에너지가 양자화된다는 뜻은?
전자가 상자 안에서 가질 수 있는 에너지는 연속적이지 않고, 계단처럼 끊어진 값을 가집니다. 이를 에너지의 양자화라고 합니다.
(1) 에너지 계산 공식

- n: 양자수 (1, 2, 3, ...)
- h: 플랑크 상수
- m: 전자의 질량
- a: 상자의 너비(장벽 사이 거리)
(2) 양자수에 따른 에너지:
- n = 1: 가장 낮은 에너지 상태(바닥 상태).
- n = 2, 3, ...: 에너지가 점점 높아지는 상태.
- n이 커질수록 전자의 에너지가 더 높아지고, 파동이 더 많이 진동합니다.

4. 전자의 위치 확률
전자는 어디에 있을 확률이 높은지 정확히 알 수는 없지만, 확률로 예측할 수 있습니다. 이 확률은 파동함수의 제곱값 |ψ(x)|²로 계산됩니다.
(1) 확률의 특징
- 파동함수는 상자 안에서 물결처럼 진동하므로, 확률도 특정 위치에서 높아지거나 낮아지는 패턴을 보입니다.
- 양자수 n이 커질수록, 즉 에너지가 높아질수록 전자가 진동하는 횟수가 많아집니다.
5. 1차원 무한에너지 장벽의 응용
- 반도체 소자 설계: 나노미터 크기의 반도체 소자에서 전자의 움직임을 이해하고 설계할 때 사용됩니다.
- 플래시 메모리: 전자가 "부유 게이트(floating gate)"라는 구조 안에 갇혀 저장됩니다. 이 원리를 설명하는 데 이 모델이 활용됩니다.
- 양자점(Quantum Dot): 나노미터 크기의 반도체 구조에서는 전자의 에너지가 양자화되며, 이 현상은 무한에너지 장벽 모델로 설명할 수 있습니다.
1차원 무한에너지 장벽은 양자역학의 대표적인 모델로, 반도체 소자와 나노 기술의 기초를 이해하는 데 큰 도움을 줍니다. 우리가 사용하는 첨단 기술의 뿌리가 되는 개념을 이해하면 더 흥미롭지 않을까요? 😊
반응형
'(비전공자)를 위한 쉬운 반도체 이야기' 카테고리의 다른 글
| 1차원 계단형 에너지 장벽에서 전자의 전파 특성 이해하기 (1) | 2025.01.17 |
|---|---|
| 1차원 유한한 에너지 장벽: 터널링 효과와 전자의 움직임 (0) | 2025.01.17 |
| 1차원 자유공간에서 전자의 움직임을 알아보다 (0) | 2025.01.17 |
| 파동방정식과 파동함수: 전자의 움직임을 읽는 열쇠 (0) | 2025.01.17 |
| 파동함수: 전자의 움직임을 그리는 수학적 지도 (0) | 2025.01.17 |



